Hi all,
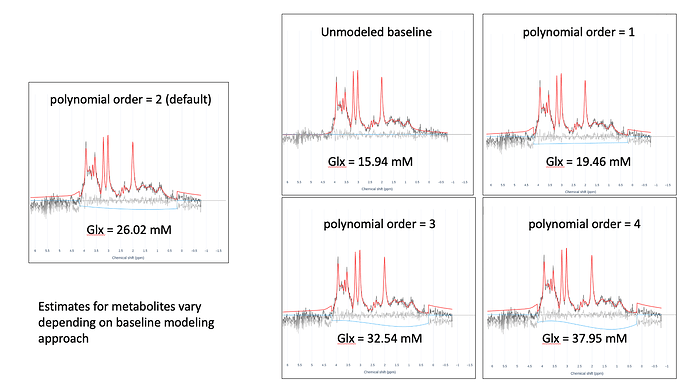
We at the Stark Lab at UC Irvine are collecting short-TE SVS from the hippocampus and are interested in performing absolute quantification with the water reference and partial volume adjustments. However, quantities seem to be highly dependent on the order of the complex polynomial baseline (fsl_mrs --baseline_order). In this example, the baseline is modeled further below zero with increasing polynomial order, causing larger estimates for Glx. Does anyone have suggestions for best practices for choosing the baseline order?
1 Like
Hi @jnlingad ,
Thanks for this detailed exploration of your data. This is something that is certainly on my list to visit again, so now may be a good time to do it. I would start off by saying that in the data you show the ‘unmodeled’ baseline (baseline_order = -1 I presume) looks not much worse a fit than any others, so I would probably proceed with that. Clearly though it’s not MSE optimal.
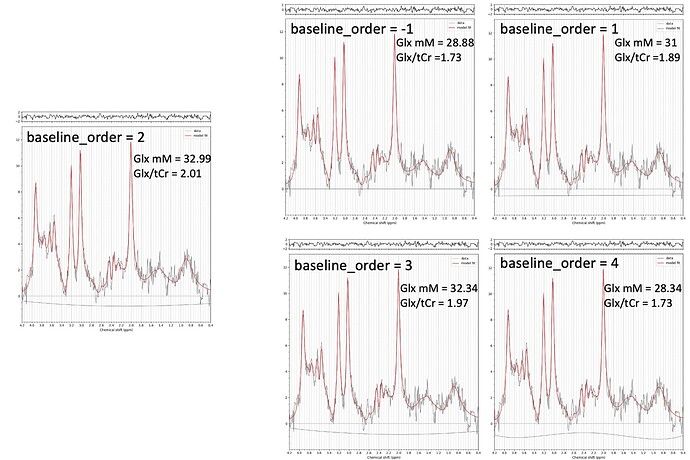
Can you tell me if the MM are being modelled using the default set or an empirically measured set? If the latter, are they getting much broadening (and are they in a separate metabolite group)? Could you also tell me if the ratio to total creatine of Glx is changing much?
Hi @wclarke,
I appreciate your response. The above example was from an older dataset that I’m hoping to salvage by exploring some of the preprocessing and fitting parameters in FSL-MRS. The hippocampus has proven to be quite a challenging region to sample from…
Here, I used the default basis set as a first pass, but I plan to use some of the empirically derived MM basis spectra shared by others here on MRSHub since our short TE spectra (40ms) have plenty of MM contamination.
I can’t seem to find that particular example to check out the ratios to tCr, so here’s another, where Glx mM or /tCr did not alter as drastically:
So far, I am visually assessing the spectrum after fitting with the default baseline order=2, and I try a different order if the baseline is far below zero and the estimated absolute concentrations are extreme. Is this the best approach here?