How to calculate the uncertainty of tNAA/tCr

[Yushan]

Hi everyone,
LCModel provides CRLB(%) of tNAA and tCr separately. So how to calculate the uncertainty of tNAA/tCr?
Is this right?

[hraum]

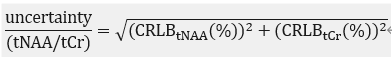
Hi Yushan,
a similar question in this thread:

Is %SD output from LCModel relevant for metabolite ratios?

Hi! I’m quite new to MRS, and carefully read the LCModel manual before initiating my analyses. As far as I understood, the stantard deviations (%SD) obtained per metabolite should be low enough to ensure reliability of the obtained metabolite concentrations, but I wonder if these are relevant as well for metabolite ratios. Thank you very much for your help! Best wishes, Diana Ortega-Cruz.

Best,
Heiner

[Yushan]

Hi Heiner,

Thank you for your prompt reply! I’ll look into it.

Best,
Yushan

[admin]

For a ratio of two variables f = \frac{A}{B} with absolute standard deviations \sigma_A and \sigma_B, covariance \sigma_{AB}=\rho_{AB}\sigma_A\sigma_B and correlation \rho_{AB} there is an approximation for the standard deviation (see Propagation of uncertainty - Wikipedia):

\sigma_f \approx \left| f \right| \sqrt{ \left(\frac{\sigma_A}{A}\right)^2 + \left(\frac{\sigma_B}{B}\right)^2 - 2\frac{\sigma_{AB}}{AB} }

Compared to the formula you posted above, the covariance term is missing. LCModel exports a correlation matrix in the .print file that should contain \rho_{AB} between tCr and tNAA (edit: it’s probably small). With the absolute CRLBs \sigma_A and \sigma_B you should be able to calculate the whole equation (not that I have ever done that before but this is probably how I’d do it).

Cheers,
Georg

PS: I just updated the forum software and, while I was at it, added the nice little MathJax plugin that allows us to write out equations like in Latex!

[Yushan]

Thank you very much, Georg!